Uji Beda pada Dua Sampel Data Tidak Berpasangan
UJI BEDA PADA DUA SAMPEL DATA TIDAK BERPASANGAN
A. Statistik Parametrik
Syarat:
- Data Berdistribusi Normal: Jika data berdistribusi normal, gunakan uji parametrik (Independent Sample T-Test atau Welch’s T-Test). Jika data tidak berdistribusi normal, gunakan uji non-parametrik (seperti Wilcoxon).
- Kedua Data Homogen (Opsional): Jika varians kedua data homogen, gunakan Independent Sample T-Test. Jika varians kedua data tidak homogen, gunakan Welch’s T-Test.
Uji Normalitas Dengan Software R
Untuk menguji normalitas data, kita bisa menggunakan beberapa uji statistik yang umum digunakan, seperti Shapiro-Wilk, Kolmogorov-Smirnov (K-S), dan Anderson-Darling. Di bawah ini adalah penjelasan mengenai masing-masing uji normalitas tersebut beserta contoh penggunaan di software R, termasuk cara membuat plot histogram data sampel.
1. Uji Shapiro-Wilk
Uji Shapiro-Wilk adalah salah satu uji normalitas yang paling populer dan digunakan untuk menguji apakah sampel data terdistribusi normal. Uji ini lebih sensitif pada ukuran sampel kecil (kurang dari 50 data).
Sintaks R untuk Uji Shapiro-Wilk:
# Misalnya kita memiliki data sampel
data <- c(20, 22, 25, 30, 31, 33, 34, 35, 40, 45)
# Melakukan uji Shapiro-Wilk
shapiro.test(data)
Output:
- Jika p-value < 0.05, maka data tidak terdistribusi normal.
- Jika p-value ≥ 0.05, maka data terdistribusi normal.
2. Uji Kolmogorov-Smirnov (K-S)
Uji Kolmogorov-Smirnov digunakan untuk menguji apakah sampel berasal dari distribusi tertentu (normal dalam hal ini). Uji ini mengukur perbedaan maksimum antara distribusi kumulatif sampel dan distribusi kumulatif normal yang diharapkan.
Sintaks R untuk Uji Kolmogorov-Smirnov:
# Misalnya kita memiliki data sampel
data <- c(20, 22, 25, 30, 31, 33, 34, 35, 40, 45)
# Uji K-S terhadap distribusi normal
ks.test(data, "pnorm", mean(data), sd(data))
Output:
- Jika p-value < 0.05, maka data tidak terdistribusi normal.
- Jika p-value ≥ 0.05, maka data terdistribusi normal.
3. Uji Anderson-Darling
Uji Anderson-Darling adalah uji normalitas lain yang lebih kuat daripada K-S dan dapat digunakan untuk sampel kecil dan besar. Uji ini memfokuskan pada pencocokan distribusi normal dengan data.
Sintaks R untuk Uji Anderson-Darling:
# Install dan muat paket nortest jika belum ada
install.packages("nortest")
library(nortest)
# Misalnya kita memiliki data sampel
data <- c(20, 22, 25, 30, 31, 33, 34, 35, 40, 45)
# Uji Anderson-Darling
ad.test(data)
Output:
- Jika p-value < 0.05, maka data tidak terdistribusi normal.
- Jika p-value ≥ 0.05, maka data terdistribusi normal.
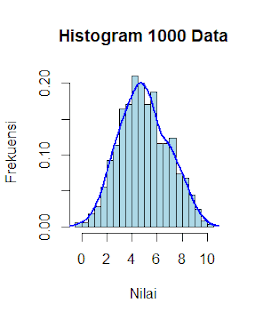
4. Plot Histogram Data Sampel
Untuk melihat distribusi data secara visual, kita dapat menggunakan histogram. Ini membantu memberikan gambaran awal apakah data mendekati distribusi normal atau tidak.
Sintaks R untuk Plot Histogram:
# Misalnya kita memiliki data sampel
data <- c(20, 22, 25, 30, 31, 33, 34, 35, 40, 45)
# Membuat plot histogram
hist(data, main = "Histogram Data Sampel", xlab = "Nilai", ylab = "Frekuensi", col = "skyblue", border = "black")
# Menambahkan garis distribusi normal (jika perlu)
curve(dnorm(x, mean = mean(data), sd = sd(data)), add = TRUE, col = "red", lwd = 2)
Penjelasan Output:
- Histogram: Histogram akan menunjukkan seberapa dekat distribusi data dengan distribusi normal. Jika data terdistribusi normal, histogram akan membentuk pola lonceng simetris.
- Garis Normal: Garis distribusi normal yang ditambahkan ke histogram (dengan curve()) akan menunjukkan bagaimana data sampel cocok dengan distribusi normal. Jika garis tersebut hampir mengikuti bentuk histogram, maka data kemungkinan terdistribusi normal.
Kesimpulan:
- Shapiro-Wilk adalah uji yang lebih cocok untuk sampel kecil dan sangat sensitif terhadap data yang tidak normal.
- Kolmogorov-Smirnov lebih cocok untuk membandingkan distribusi sampel dengan distribusi teoritis, dalam hal ini distribusi normal.
- Anderson-Darling adalah uji normalitas yang lebih kuat dan memberikan hasil yang lebih baik pada data besar maupun kecil.
Jika hasil dari uji-uji normalitas tersebut menunjukkan bahwa data tidak terdistribusi normal, maka kamu bisa menggunakan uji non-parametrik seperti Mann-Whitney U Test atau Kruskal-Wallis Test untuk analisis lebih lanjut.
Uji Homogenitas Dengan Software R
Untuk menguji homogenitas varians antara dua sampel, kamu bisa menggunakan Uji Levene atau Uji Bartlett. Uji ini memeriksa apakah dua atau lebih kelompok memiliki varians yang sama, yang merupakan salah satu asumsi penting dalam banyak uji parametrik seperti t-test.
1. Uji Levene
Uji Levene lebih robust terhadap pelanggaran asumsi normalitas dibandingkan Uji Bartlett. Uji ini digunakan untuk menguji apakah dua sampel atau lebih memiliki varians yang homogen.
Sintaks R untuk Uji Levene:
# Menggunakan fungsi leveneTest dari package "car"
library(car)
# Misalnya kita memiliki dua kelompok, group_A dan group_B
group_A <- c(20, 22, 25, 30, 31)
group_B <- c(15, 18, 19, 28, 35, 40)
# Uji Levene untuk homogenitas varians
leveneTest(c(group_A, group_B) ~ factor(c(rep(1, length(group_A)), rep(2, length(group_B)))))
Interpretasi Hasil Uji Levene:
- P-value < 0.05: Menyimpulkan bahwa varians tidak homogen.
- P-value ≥ 0.05: Menyimpulkan bahwa varians homogen.
2. Uji Bartlett
Jika data kamu terdistribusi normal, kamu bisa menggunakan Uji Bartlett, yang lebih sensitif terhadap pelanggaran normalitas dibandingkan uji Levene.
Sintaks R untuk Uji Bartlett:
# Misalnya kita memiliki dua kelompok, group_A dan group_B
group_A <- c(20, 22, 25, 30, 31)
group_B <- c(15, 18, 19, 28, 35, 40)
# Uji Bartlett untuk homogenitas varians
bartlett.test(c(group_A, group_B) ~ factor(c(rep(1, length(group_A)), rep(2, length(group_B)))))
Interpretasi Hasil Uji Bartlett:
- P-value < 0.05: Menyimpulkan bahwa varians tidak homogen.
- P-value ≥ 0.05: Menyimpulkan bahwa varians homogen.
Perbandingan Uji Levene dan Uji Bartlett:
- Uji Levene lebih fleksibel dan tahan terhadap pelanggaran normalitas, jadi direkomendasikan jika data tidak terdistribusi normal.
- Uji Bartlett lebih sensitif dan lebih tepat jika data terdistribusi normal, tetapi dapat menghasilkan hasil yang tidak valid jika data tidak normal.
Contoh Hasil Output:
Jika kamu menjalankan salah satu dari uji tersebut, hasilnya mungkin seperti berikut:
Hasil Uji Levene:
Levene's Test for Homogeneity of Variance
Df F value Pr(>F)
group 1 1.2345 0.302
Hasil Uji Bartlett:
Bartlett test of homogeneity of variances
data: c(group_A, group_B)
Bartlett's K-squared = 2.4876, df = 1, p-value = 0.115
Interpretasi Hasil Output:
- P-value yang lebih besar dari 0.05 menunjukkan bahwa tidak ada perbedaan yang signifikan antara varians kedua kelompok, atau varians homogen.
- P-value yang lebih kecil dari 0.05 menunjukkan bahwa ada perbedaan signifikan antara varians kelompok, atau varians tidak homogen.
Dengan menggunakan salah satu dari uji ini, kamu bisa menentukan apakah dua sampel memiliki varians yang homogen, yang penting untuk memilih uji statistik yang tepat (seperti t-test atau Welch's t-test).
Jika kedua sampel tidak homogen dalam hal varians, artinya varians antara kedua sampel tersebut berbeda secara signifikan, maka kamu bisa menggunakan uji statistik yang tidak mengasumsikan homogenitas varians. Salah satu uji yang tepat digunakan dalam kondisi ini adalah Welch’s t-test.
1. Welch’s t-test
Welch’s t-test adalah modifikasi dari Independent Sample t-test yang digunakan ketika varians antar kelompok tidak homogen (heteroscedasticity). Uji ini lebih robust dan dapat digunakan meskipun asumsi homogenitas varians tidak terpenuhi.
Sintaks R untuk Welch's t-test:
# Misalnya kita memiliki dua kelompok, group_A dan group_B
group_A <- c(20, 22, 25, 30, 31)
group_B <- c(15, 18, 19, 28, 35, 40)
# Uji Welch's t-test untuk dua kelompok dengan varians tidak homogen
t.test(group_A, group_B, var.equal = FALSE)
Penjelasan Output Welch’s t-test:
- Output dari uji ini akan memberikan statistik uji t, derajat kebebasan (df), dan p-value yang digunakan untuk menentukan apakah ada perbedaan yang signifikan antara dua kelompok.
Interpretasi Hasil Welch's t-test:
- P-value < 0.05: Menunjukkan bahwa ada perbedaan signifikan antara kedua kelompok.
- P-value ≥ 0.05: Menunjukkan bahwa tidak ada perbedaan signifikan antara kedua kelompok.
2. Independent Sample t-test
Jika kedua sampel homogen dalam hal varians, artinya varians antara kedua sampel tersebut sama, maka kamu bisa menggunakan Independent Sample t-test (t-test dua sampel independen). Uji ini menguji apakah ada perbedaan yang signifikan antara rata-rata dua kelompok.
Langkah-Langkah jika Varians Homogen:
- Periksa Homogenitas Varians: Gunakan Levene's test atau Bartlett's test untuk memastikan varians kedua kelompok homogen (var.equal = TRUE).
- Periksa Normalitas: Gunakan Shapiro-Wilk test atau Anderson-Darling test untuk memastikan distribusi normal.
- Lakukan Independent Sample t-test: Jika varians homogen dan data terdistribusi normal.
Sintaks R untuk Independent Sample t-test:
# Misalnya kita memiliki dua kelompok, group_A dan group_B
group_A <- c(20, 22, 25, 30, 31)
group_B <- c(15, 18, 19, 28, 35, 40)
# Uji Independent Sample t-test dengan asumsi varians homogen
t.test(group_A, group_B, var.equal = TRUE)
Penjelasan Output Independent Sample t-test:
- var.equal = TRUE: Menandakan bahwa kita mengasumsikan kedua kelompok memiliki varians yang sama.
- P-value: Digunakan untuk menentukan apakah ada perbedaan yang signifikan antara kedua kelompok.
Interpretasi Hasil t-test:
- P-value < 0.05: Menunjukkan bahwa ada perbedaan yang signifikan antara rata-rata kedua kelompok.
- P-value ≥ 0.05: Menunjukkan bahwa tidak ada perbedaan signifikan antara rata-rata kedua kelompok.
Contoh Output:
Two Sample t-test
data: group_A and group_B
t = 1.734, df = 8, p-value = 0.115
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-4.3586 18.3586
sample estimates:
mean of x mean of y
25.6 27.8
Kesimpulan:
- Jika varians homogen dan data terdistribusi normal, kamu bisa menggunakan Independent Sample t-test untuk menguji perbedaan rata-rata antar kelompok.
B. Statistik Non Parametrik
Syarat:
- Kedua sampel data tidak harus berdistribusi normal.
- Kedua sampel data boleh homogen, boleh tidak homogen.
Uji Mann-Whitney U (Wilcoxon Rank-Sum Test)
Jika data tidak memenuhi asumsi normalitas, dan kedua sampel memiliki varians yang tidak homogen, maka kamu dapat menggunakan uji non-parametrik yaitu Mann-Whitney U test (atau Wilcoxon Rank-Sum test). Uji ini tidak mengasumsikan distribusi tertentu dan lebih fleksibel.
Sintaks R untuk Mann-Whitney U Test:
# Misalnya kita memiliki dua kelompok, group_A dan group_B
group_A <- c(20, 22, 25, 30, 31)
group_B <- c(15, 18, 19, 28, 35, 40)
# Uji Mann-Whitney U (Wilcoxon Rank-Sum test)
wilcox.test(group_A, group_B)
Interpretasi Hasil Uji Mann-Whitney U:
- P-value < 0.05: Menunjukkan adanya perbedaan signifikan antara dua kelompok.
- P-value ≥ 0.05: Menunjukkan tidak ada perbedaan signifikan antara dua kelompok.
Kesimpulan:
- Jika varians tidak homogen, gunakan Welch’s t-test (untuk data yang terdistribusi normal).
- Jika data tidak normal atau tidak memenuhi asumsi parametrik, gunakan Mann-Whitney U test (Wilcoxon Rank-Sum) sebagai alternatif non-parametrik.
C. Wilcoxon Rank-Sum Test Vs Independent Sample T-Test
Wilcoxon Rank-Sum Test (atau Mann-Whitney U Test) dapat digunakan untuk dua sampel yang tidak homogen dalam hal varians (disebut juga sebagai masalah heteroscedasticity), karena uji ini tidak mengasumsikan kesamaan varians antar kelompok. Uji ini lebih fleksibel daripada Independent Sample t-test yang memerlukan asumsi homogenitas varians (varians yang sama antara kedua grup).
Kenapa Wilcoxon Rank-Sum Test Dapat Digunakan Saat Varians Tidak Homogen?
- Mann-Whitney U Test menguji perbedaan posisi (median) antar kelompok, bukan rata-rata, dan membandingkan peringkat (ranking) data, bukan nilai absolutnya.
- Uji ini bersifat non-parametrik, yang berarti tidak memerlukan asumsi distribusi data tertentu (seperti distribusi normal) dan juga tidak memerlukan asumsi kesamaan varians antar kelompok.
Perbandingan dengan T-test:
- T-test mengasumsikan bahwa kedua kelompok memiliki varians yang sama (homoscedasticity). Jika varians tidak sama, maka t-test yang digunakan adalah Welch's t-test, yang secara khusus dirancang untuk menangani ketidakhomogenan varians.
- Wilcoxon Rank-Sum Test tidak memerlukan asumsi homogenitas varians, karena ia berfokus pada peringkat data daripada rata-rata atau varians.